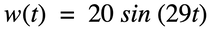Blog Archives

Friday Solve for the Flying Delorean 1/31/20

1/31/2020

Objective: Use vectors and equations for falling objects to find where the Flying Delorean will land.

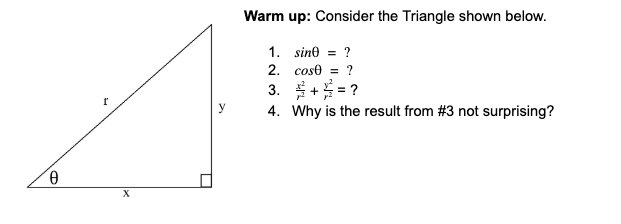
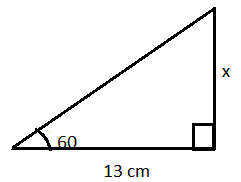
Warm up: Review the following things we did yesterday and Tuesday.

Explain the free body diagram of the Flying Delorean
List all of the equations we found for a falling object with an initial velocity.

Solve for the Flying Delorean:

Find the vertical and horizontal initial velocity
Find the air time of the Flying Delorean
Use the air time to find the horizontal distance traveled

Tuesday 1/27/20

1/27/2020

Objective: Understand vectors by connecting it to the Flying Delorean Problem.

Vectors Activity

Definition: Quantity represented by direction and magnitude
Ex. Velocity: 5 m/h North
Ex. 4i-7j+13k
Ex. Matrix vector
Ex. (1,2) (4,5,-3)

Stations

Instructions: For this activity, on the tables around the room are worksheets that have instructions for the different workstations. Once you get to your table, find the instruction sheet and the activity that goes with it. Each activity will be given 12 minutes to complete, once you completed all 6 stations turn in this worksheet to Ande.

Materials: Notebook, Computer, Desmos

Table 1: Scavenger Hunt
Task: You must find the yeeted cat. Follow these vectors until you find it. Use a compass and count your steps to measure the vectors. The yellow wall in Kyle’s room represents the x-axis while the hallway outside the classroom represents the y-axis. The door is considered the origin. Use the examples of vectors to find the yeeted cat.

Table 2: Vector Operations

Listen to Ande’s or Kyle’s Lecter on vector operations.

-Adding/Subtracting Vectors
-Scalar multiplication
-magnitude

Complete to practice problems on your Vector Activity Worksheet

Table 3: Climbing Anchors
Task: The goal of this activity is to calculate force on anchor points for climbing anchors. On the rack, there are three configurations of anchors and a weight suspended from each focal point. Calculate the amount of weight on each anchor point.

Table 4: Vector Fields
https://www.intmath.com/blog/mathematics/vector-fields-a-simple-and-painless-introduction-3345
Instructions:

Open Ande’s DP and clink the link under Table 4.
Read The article
Answer the prompt on your Vector Activity Worksheet

Table 5: Free Body Diagrams
Task: In the video the guy gives various examples of free body diagrams. When you see the pause symbol on the screen stop the video and draw the free body diagram. Do this for 3 examples.
Instructions:

Open Ande’s DP and clink the link under Table 5.
Watch this video: https://www.youtube.com/watch?v=nDis6HbXxjg
Draw 3 free body diagrams from the video

Table 6: Free Body Diagram of the Flying Delorean
Task: From Table 5 you learned how to create free body diagrams. This will be very useful for determining where the flying delorean will land. Follow the prompts below.

Measure how fast the Delorean goes down the ramp. This is the initial velocity.
Assume when the Flying Delorean leaves the ramp it is t=0. Draw free body diagram of the Flying Delorean
What is the vertical and horizontal components of the vector of the Flying Delorean’s initial velocity?

Monday 1/27/20

1/26/2020

Objective:

Understand how initial velocity influences velocity, distance, and acceleration of falling objects.

Warm-up:

What is the quadratic formula?
What is it used for?

HW Due: Falling Objects Worksheet EOC

Initial Velocity:

finish table 2

2. Update formulas
Distance to ground dg (solve for t using quadratic formula)
Time it takes to hit the ground: tf

Problem of the Week: The Flying Delorean

Now that we have formulas that can describe an object’s position, speed, and acceleration with a given initial velocity it is now time to apply it to a real life problem. Consider this ramp and a car rolling down the ramp and then off a cliff. Or in this case this ramp will be on the roof of the school. You will be tasked with figuring out exactly where the car will land by placing a dixie cup. This is a competition and the table group that predicts the right spot wins.

Task: Draw a diagram of The Flying Delorean and include the following:

What is the goal of this problem?
List the variables that will be involved
List formulas that will be involved
What measurements will need to be made?
What is one thing you are confused about or foresee being a challenge?

Thursday 1/23/20

1/22/2020

Objective: Understand the characteristics of free falling object from rest by exploring position, velocity, and acceleration.

Warm-up:
Without looking it up, write a definition for the following terms:

Velocity:

Instantaneous Velocity:

Average Velocity:

Acceleration:

Free Fall Activity: The purpose of this activity is to explore the characteristics of falling objects using math. Below is a link to the document.

Free Fall Worksheet

Tuesday 1/21/20

1/21/2020

Objective: Apply the sine function in a real world problem.

Sand Castles:
Ande loves to build elaborate sand castles at the beach. In fact, he is so skilled at making them they often take a long time to build. But sadly, the tides come in and demolish Ande’s work of art.

Since Ande has a mathematical mind he has spent scrupulous time modeling the tides at the beach. According to his analysis, the equation of the tides goes as follows:

w(t)represents the waterline above and below its average position
t represents time
The function represents the waterline for a 24 hour period

Your Task:
Ande needs to be closer to the waterline to maximize his skills building a sand castle.

If he builds 10ft below the waterline, what time should he come to the beach to maximize building time?
How is the tide changing over time, what is the average rate of change of the tide?

Friday 1/17/20

1/16/2020

Warm up:

At your table groups make sure you understand what does A, B, h, and k do with y=Asin(B(x-h))+h.
In the real world, name 3 things you can find waves?

Master Spreadsheet Part 1:
In your table group, create a spreadsheet and this will be your tool to solve the unit problem. This spreadsheet should contain the following:
Inputs:

Ferris wheel with any radius r
Ferris wheel takes t seconds to complete on revolution
Ferris wheel with center at height h
Amount of time for one rotation

Output:

Any y position given time t
Any x position given time t
angular speed

Math and Music

Sine and Cosine Exploration:
Below are some links to some cool ways trigonometric functions can be represented and applied. During the remainder of class explore these links and see how cool sine and cosine can be.

Homer Simpson Fourier
Trig Gifs

Thursday 1/16/20

1/15/2020

Objective: Explore the characteristics of sine and cosine graphically

Ferris Wheel Activity:

Email your HW to ANDE
Check the board for answers
Questions?

Desmos Activity: Pull up Desmos and graph y = Asin(B(x-h))+k. Add sliders for A, B, h, and k. Copy and paste these questions on a separate document and answer the following questions. I recommend recording the definitions in your notes.
For the following terms write the definition of the term, then state which slider in your function changes it:

Midline
Amplitude
Period
There is one more slider that changes the function, how does this slider change the function?
Graph a cosine wave where it matches with your sine wave, what did you change to make it match up?

Wednesday 1/15/20

1/14/2020

Objective: Generalize a formula for the ferris wheel's height in the first quadrant.

Warm up: Find the length of the side x on the right triangle shown below.

Board Work: Suppose a ferris wheel with a radius of 50 feet, and is 65 feet above the ground and completes one revolution in 40 seconds.

Find the vertical and horizontal position for every 30 degree interval for one revolution.
Graph the vertical and horizontal positions for one revolutions.
Create a formula that models the platforms vertical position over time, and horizontal position over time.

Homework: Complete the Ferris Wheel Activity found under Tuesday's lesson.

Tuesday 1/14/20

1/13/2020

Objectives:

Understand how to find all the sides of a right triangle using soh, cah, toa.
Convert radians to degrees and degrees to radians.
Apply triangles to finding the height on a ferris wheel at certain angles.

Warm up: Desmos Debut

https://www.desmos.com/calculator/m9mnykyrvc

Lecture:

Using Soh Cah Toa to solve right Triangles
Converting Radians and Degrees

Complete the worksheet of practice problems found here. Due at the end of class.

Ferris Wheel Activity: Due Thursday 1/16/20
Consider a ferris wheel with a radius of 50 feet and turns at a constant speed. The center of the ferris wheel is 65 feet off the ground and takes 40 seconds to complete one revolution and turns counter clockwise. Copy and paste this problem on a separate document and answer the following questions.

How high off the ground are the passengers when they are at the following positions?
1. 3 o’ clock position
2. 12 o’ clock position
3. 2 o’ clock position
4. 11 o’ clock position
5. 4 o’ clock position
What is the speed (in feet per second) of the passengers as they go around this ferris wheel?
Look up the definition of angular speed, what is the angular speed of this ferris wheel?
How many seconds does it take to for the passengers to go each of these distances?
1. 3 o’ clock to 11 o’ clock
2. 3 o’ clock to 7 o’ clock

January 10th, 2020

1/10/2020

Objective: Investigate the Unit problem

Warm up:

Consider a ferris wheel and you want to model the vertical position of a passenger over time. Note as the ferris wheel spins, the passengers vertical and horizontal speed is not constant. Given positions a, b, c, and d, rank the vertical speed from fastest to slowest.

Unit Problem Activity:
Directions:

(3 min) Read pages 4-5 in the textbook
At your tables there is a supply of materials, make a physical model of the problem
Specify any information you need to know about the circus act to determine when the assistant should let go.

Guiding Questions:

What are the variables in this problem?
What do you expect will be the most challenging task in solving this problem?
What is the next step?

<<Previous